Lattice-based zero-knowledge proofs (ZKPs) offer a path toward quantum-resistant and scalable blockchain systems. Unlike traditional cryptographic approaches, lattice-based ZKPs rely on those mathematically hard problems for which no efficient quantum attack algorithms are known, such as Learning With Errors (LWE) and Short Integer Solutions (SIS). These constructs are more than just theoretical: they are unlocking new efficiencies in privacy-preserving technologies and secure computation.

This article examines the foundational role of lattices in cryptography, their application in ZKPs, and groundbreaking research shaping the field. It also highlights how these advances may impact the blockchain space, from zk-rollups to decentralised identity systems, paving the way for innovative use cases across Web3 ecosystems.

TL;DR – Lattice-Based Zero-Knowledge Proofs (ZKPs)

• Post-Quantum Security: Lattice-based ZKPs rely on hard problems like LWE and SIS, offering resilience against quantum attacks and forming the basis for cryptographic primitives such as commitments and arguments of knowledge.

• ZK Applications: These constructions enable succinct, non-interactive proofs suited for zk-rollups, privacy-preserving smart contracts, and decentralized identity systems.

• Research Momentum: Systems like LaZer, LatticeFold, and Greyhound demonstrate advances in polynomial commitments, folding schemes, and efficient ZK proof generation under lattice assumptions.

• Performance Tradeoffs: Compared to traditional ZKPs, lattice-based systems face higher proof sizes and slower verification, posing challenges for recursive proofs and scalability.

• FHE Synergy: Compatibility with fully homomorphic encryption (FHE) supports operations on encrypted data, expanding applicability to verifiable computation and privacy-preserving protocols. 

First, What’s a Lattice?

A lattice is a mathematical construct that can be visualised as a repeating grid of points in space, extending infinitely in all directions. These points are generated by adding together integer multiples of a set of linearly independent vectors, called the basis vectors. While a lattice might look like a simple checkerboard in two dimensions, cryptographic lattices operate in much higher-dimensional spaces, often involving hundreds or thousands of dimensions. This complexity is what makes them useful for cryptography.

What Role Do Lattices Play in Cryptography? 

Lattices and in particular high-dimensional integer lattices, are interesting for cryptography since there are certain computational problems over lattices for which no efficient solving algorithms are known. Specifically, these problems exploit properties such as the geometric arrangement of lattice points and the difficulty of finding short vectors within this discrete structure. Two of the most prominent problems are the Learning With Errors (LWE) problem and the Short Integer Solutions (SIS) problem. Both are believed to be hard due to reductions from worst-case lattice problems, like the Shortest Vector Problem (SVP), to their average-case instances, ensuring security even in the presence of quantum adversaries.

LWE involves solving systems of linear equations where small random errors have been added, making the problem computationally infeasible to reverse. On the other hand, SIS focuses on finding particularly small solutions to a set of linear constraints. Both problems have been extensively studied and form the backbone of lattice-based cryptographic systems.

Lattices are particularly attractive in cryptography because their hardness assumptions remain robust even against quantum computers. This post-quantum security sets them apart from traditional cryptographic systems like RSA and elliptic curve cryptography, which are vulnerable to quantum attacks. Furthermore, lattices enable various advanced cryptographic applications, including fully homomorphic encryption and, increasingly, zero-knowledge proofs.

How Can Lattices Help ZK?

Zero-knowledge proofs (ZKPs) are cryptographic protocols that allow one party, the prover, to convince another party, the verifier, that they know a piece of information or have performed a computation without revealing any details. In lattice-based cryptography, ZKPs leverage the mathematical hardness of lattice problems to construct secure and efficient proof systems.

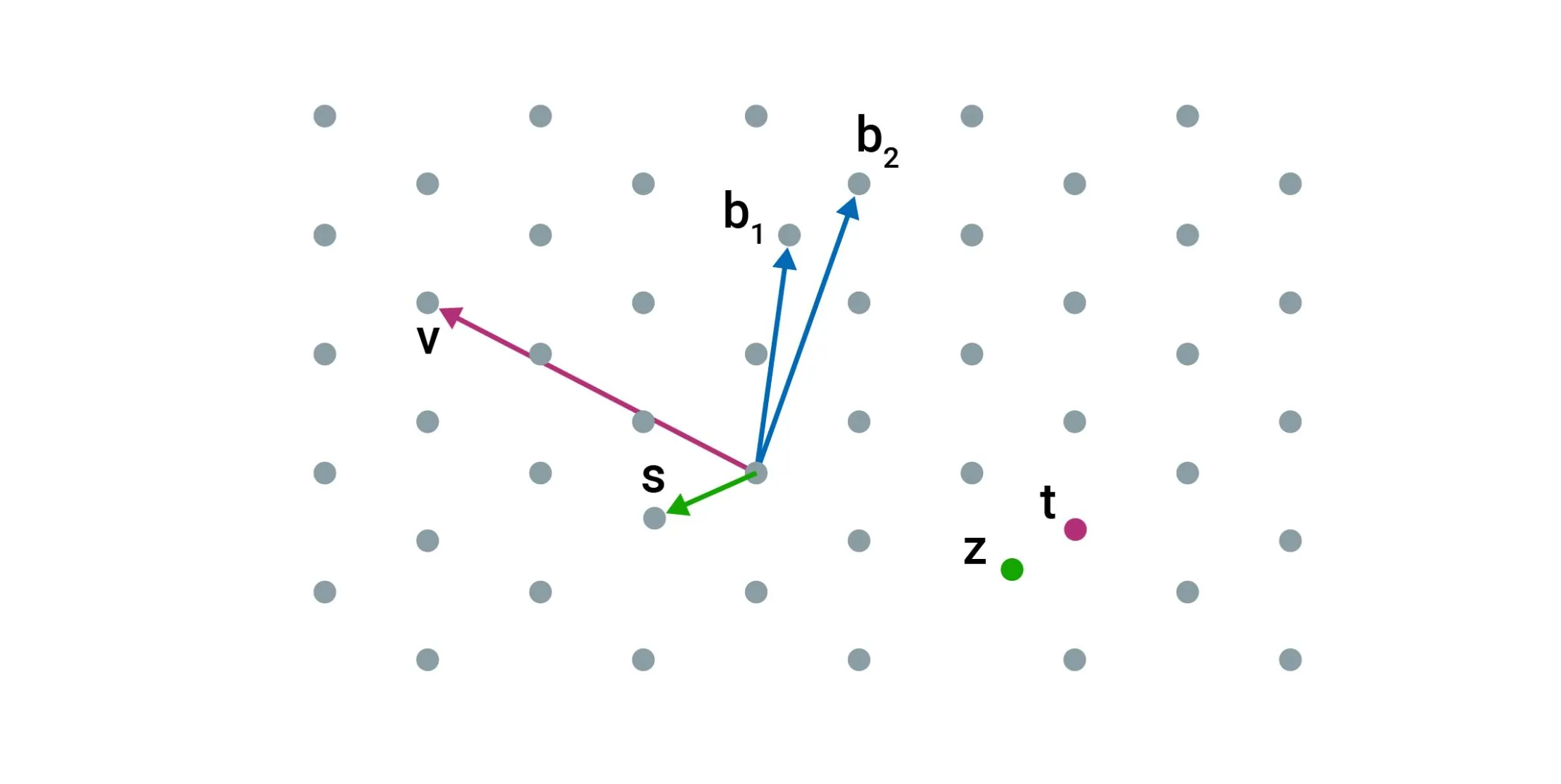
One key application of lattices in ZKPs is in commitment schemes. These fundamental building blocks of ZKPs allow a prover to “commit” to a value while keeping it hidden. The prover can later “open” the commitment to reveal the value, but the scheme’s structure ensures they cannot change their mind about the value once committed. Lattice-based commitment schemes often rely on the SIS problem to ensure that the commitment is both binding (unchangeable) and hiding (secret).

Lattices also play a crucial role in building arguments of knowledge. In these protocols, the prover demonstrates that they possess a solution to a hard lattice problem—such as a particularly short vector in a lattice—without revealing the solution itself. The security of these arguments comes from the mathematical difficulty of reversing the lattice-based operations involved.

The advantages of lattice-based ZKPs are notable. They are believed to resist quantum attacks, making them a promising choice for long-term security in blockchain applications. Additionally, lattice-based constructions have the potential to enable more efficient proof systems, although this area of research is still evolving. Perhaps most intriguingly, lattices offer the flexibility to design novel ZK protocols, including succinct and non-interactive proofs. These are particularly well-suited for blockchain use cases like zk-rollups and privacy-preserving smart contracts.

Research Trends in Lattice-based ZK

Lattice-based zero-knowledge proofs (ZKPs) have emerged as a promising area of cryptographic research, driven by the need for post-quantum secure systems and the potential for performance improvements. Recent developments highlight a shift toward leveraging lattice structures for building polynomial commitment schemes, SNARKs, and folding mechanisms, all of which play critical roles in modern ZK applications.

In addition to security, lattice-based constructions are being explored for their unique capabilities. For example, they naturally align with fully homomorphic encryption (FHE), enabling efficient operations on encrypted data. This synergy allows lattice-based ZKPs to play a dual role: providing cryptographic guarantees for privacy and facilitating integrity checks on computations performed in encrypted domains.

The past two years have seen significant advances in this field. Notable works like Labrador and Greyhound have introduced lattice-based polynomial commitment schemes and ZK systems that push the scalability boundaries. These schemes have demonstrated the ability to handle large polynomials while maintaining proof succinctness, albeit with challenges in verifier efficiency. Another breakthrough is lattice-based folding schemes, which simplify the generation of ZK proofs by breaking large problems into smaller, manageable pieces.

Despite their promise, lattice-based ZKPs face several hurdles, including slower verification times and higher proof sizes than traditional methods. These limitations challenge recursive ZK applications and high-throughput systems, making ongoing optimisation efforts critical.

As research progresses, integrating lattice-based ZKPs into blockchain systems offers an opportunity to create post-quantum secure privacy-preserving applications. Their compatibility with emerging hardware optimisations for FHE may further accelerate adoption, paving the way for innovative solutions in zk-rollups, decentralised identity systems, and cross-chain interactions.

Latest Research in Lattice-based ZK

Here are some of the latest, most prominent papers that use Lattices and ZK. 

ZK Proofs 

Lattice-Based SNARGs by Dan Boneh, Yuval Ishai, Amit Sahai, and David J. Wu: This work presents lattice-based SNARGs (Succinct Non-Interactive Arguments) with quantum-resistant security based on Learning with Errors (LWE). It introduces linear-only vector encryption to enforce prover constraints, enabling quasi-optimal succinctness and efficiency. The authors further apply these SNARGs to program obfuscation, reducing the multilinearity degree of multilinear maps by over 280x compared to existing approaches. This innovation advances the practicality of secure obfuscation and lattice-based cryptography, offering efficient proofs and resistance to quantum attacks while addressing key limitations in current obfuscation frameworks.

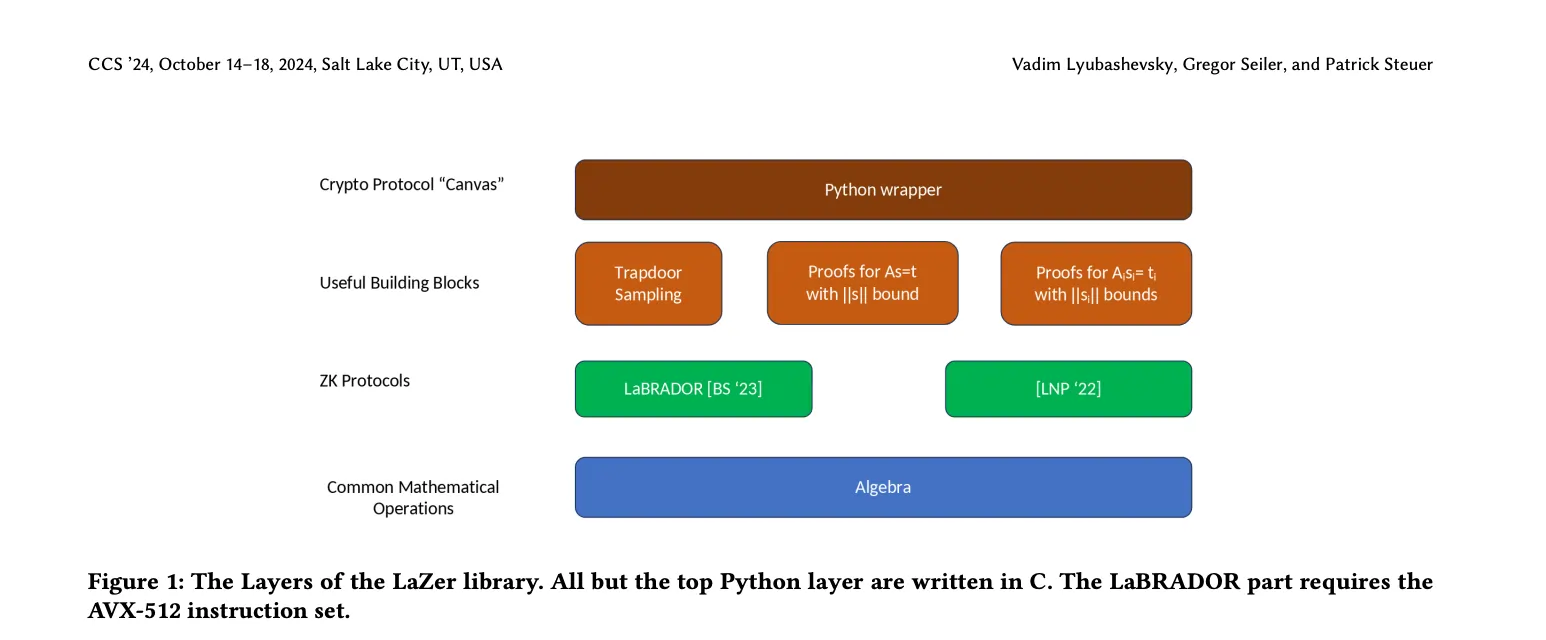
LaZer library by Vadim Lyubashevsky, Gregor Seiler, Patrick Steuer: The LaZer Library facilitates lattice-based zero-knowledge (ZK) and succinct proof systems tailored for quantum-safe cryptography. It provides a Python interface for creating ZK proofs, enabling users to define lattice relations and norm bounds, with the library automating parameter tuning and proof generation. LaZer integrates linear-size proofs and LaBRADOR succinct proofs, optimised for applications like blind signatures and aggregate signatures. It supports flexible protocols, leveraging quantum-resistant assumptions such as LWE and SIS, and offers efficient implementations using AVX-512 instructions. The library aims to bridge usability gaps in lattice-based cryptography while maintaining high efficiency and compact proofs.

Folding Schemes

Lova by Giacomo Fenzi, Christian Knabenhans, Ngoc Khanh Nguyen, Duc Tu Pham: Lova introduces a lattice-based folding scheme based on the unstructured SIS assumption, enabling incrementally verifiable computation (IVC) with minimal norm growth and efficient verification. Using a decompose-and-fold paradigm and a novel Euclidean norm proof, it avoids reliance on structured lattice assumptions or complex finite field arithmetic. Hardware-friendly optimisations, such as power-of-two moduli, enhance computational efficiency. The approach facilitates quantum-resistant applications, including succinct blockchains and verifiable delay functions, while advancing lattice-based cryptographic techniques for secure and practical proof systems.

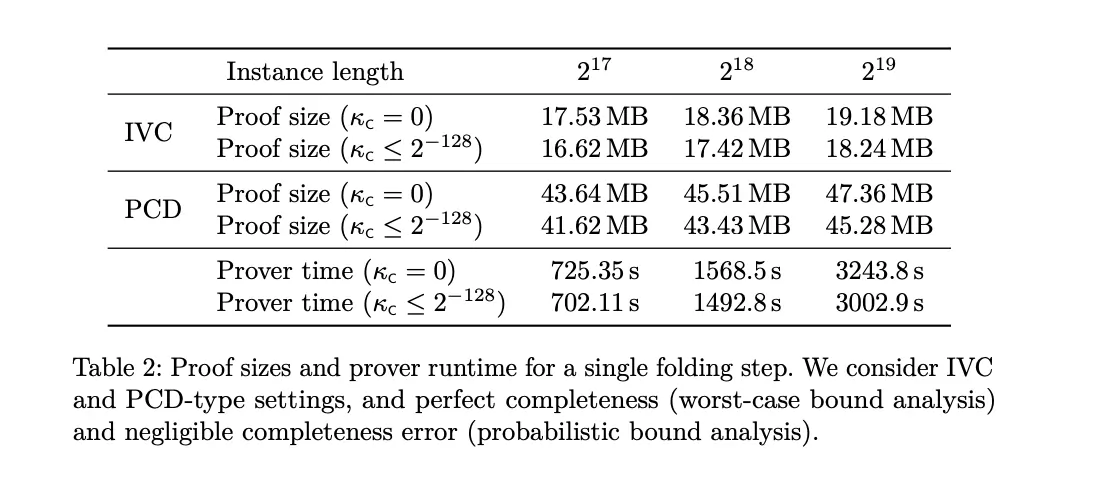
LatticeFold & LatticeFold+ by Dan Boneh, Binyi Chen: LatticeFold and LatticeFold+ are sequential lattice-based folding schemes authored by the same research group, both targeting succinct proof systems with post-quantum security grounded in the Module Short Integer Solution (MSIS) problem. LatticeFold introduces a folding framework compatible with both R1CS and CCS relations, using Ajtai commitments and a novel sumcheck-based norm-bounding technique to manage witness norm growth in recursive proof construction. It operates over small prime moduli to improve hardware efficiency and achieves performance on par with SNARKs like Hypernova. A Rust implementation was recently released by Nethermind.

LatticeFold+ extends this framework by replacing bit-decomposition-based range proofs with a more efficient algebraic range proof mechanism and incorporating double commitments. These modifications significantly reduce prover time (by 5–10×), lower verifier circuit complexity, and produce shorter proofs. LatticeFold+ maintains post-quantum security under the same lattice assumptions while optimizing prover performance and preserving knowledge soundness.

Commitment Schemes

Orbweaver by Ben Fisch, Zeyu Liu, Psi Vesely: Orbweaver introduces a lattice-based functional commitment for linear relations that supports quasilinear prover time, logarithmic proof size, and polylogarithmic verifier time. Using the k-R-ISIS assumption and its knowledge counterpart enables extractable commitments with compact public proof aggregation. Orbweaver supports linear function evaluations over cyclotomic rings, achieving post-quantum security and proof sizes smaller than prior lattice-based systems. Applications include univariate and multilinear polynomial commitments, with extensions to enable succinct aggregation and efficient verification for large circuits. The scheme demonstrates advancements in lattice-based cryptography for succinct and scalable proof systems.

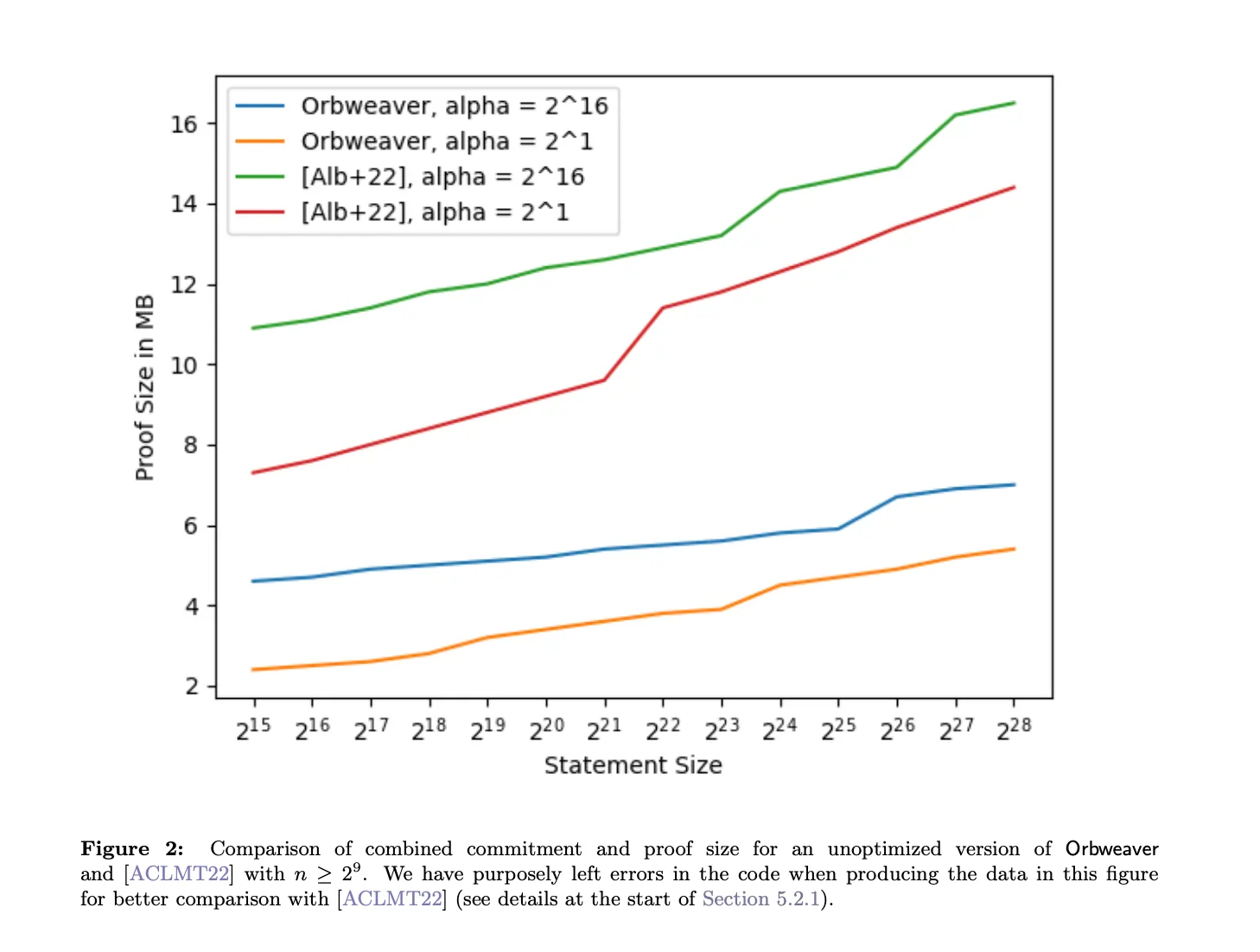
GreyHound Ngoc Khanh Nguyen, Gregor Seiler: Greyhound is a lattice-based polynomial commitment scheme built on the Module-SIS assumption, achieving post-quantum security. It provides quasilinear proof generation, polylogarithmic proof sizes, and sublinear verification time for bounded-degree polynomials. Unlike prior schemes, Greyhound eliminates the need for a trusted setup and offers proofs 104 times smaller than SLAP (EUROCRYPT 2024) for large polynomials, with significant commitment and proving time speedups. The scheme incorporates an AVX-512 optimised library for fast polynomial arithmetic, demonstrating practicality for quantum-resistant SNARKs, verifiable secret sharing, and multi-party computation.

Conclusions 

Integrating lattice-based zero-knowledge proofs into cryptographic systems signals a profound shift in blockchain and Web3 infrastructure. These systems provide long-term resilience against quantum threats and enable novel applications that blend privacy, scalability, and interoperability. From polynomial commitment schemes to efficient folding techniques, recent research is bridging the gap between mathematical theory and practical blockchain use cases.

Yet, the path forward is not without challenges. Slower verification times, larger proof sizes, and deployment complexity remain significant hurdles. Addressing these inefficiencies will be critical for lattice-based ZKPs to move beyond niche applications and become foundational to blockchain networks.

Despite these barriers, the trajectory of lattice-based research reflects steady progress. The synergy between lattice-based ZKPs and fully homomorphic encryption (FHE) opens doors to breakthroughs in verifiable computations, identity protocols, and decentralised financial systems. For blockchain developers and researchers, lattice-based ZKPs offer a quantum-secure foundation for building the next generation of decentralised infrastructure.