In the last quarter, we have seen a rising interest in coSNARKs. With this article, we want to dive a bit deeper into what coSNARKs are and how they can help shape the future of ZK.

TL;DR

• coSNARKs enable multi-party zk-SNARK proofs over distributed secrets without revealing individual inputs.
• Introduces “MPC-friendliness” to assess zk-SNARKs’ efficiency in collaborative settings.
• Groth16, Marlin are highly MPC-friendly; Plonk moderate; Fractal less so due to hashing overhead.
• Real-world applications include healthcare, credit scoring; production tooling includes Co-Circom, coNoir.

coSNARKs: The What, the How, and the Why

Let’s start by breaking down what coSNARKs are.

coSNARKs, or collaborative zk-SNARKs, expand the capabilities of traditional zk-SNARKs by enabling multiple parties, each holding a piece of secret information, to work together to produce a single proof. This proof certifies the validity of a public statement without revealing the individual secrets of any participant. While standard zk-SNARKs are designed for scenarios where one party holds the entire witness (the private data used to construct the proof), coSNARKs tackle the challenge of distributed witnesses—a common requirement in real-world applications.

Why Are coSNARKs Needed?

Dan Boneh and Alex Ozdemir, researchers at Stanford University specializing in cryptography and secure computation, introduced collaborative zk-SNARKs (coSNARKs) to address inherent limitations in applying conventional zk-SNARKs to multi-party settings. In their 2021 work, they observed that traditional zk-SNARKs assume the witness is entirely held by a single party, which does not reflect the requirements of many real-world scenarios where sensitive information is distributed across multiple entities. For instance, they describe healthcare systems, where providers must prove aggregate statistics over patient data without compromising individual privacy. Similarly, in financial systems, institutions computing credit scores collaboratively face the challenge of preserving the confidentiality of their respective datasets. Without a protocol like coSNARKs, these problems necessitate pooling sensitive data into a central repository, which raises both privacy and trust concerns. 

How coSNARKs Work?

To solve this, the authors reimagined zk-SNARKs as a collaborative effort, combining them with secure multi-party computation (MPC). This allowed multiple provers to jointly generate a proof while keeping their individual inputs hidden. Importantly, they didn’t stop at feasibility—they optimised the process to make collaborative proofs efficient, even in complex settings. Along the way, they introduced the concept of “MPC-friendliness,” highlighting that not all zk-SNARKs are equally suited for distributed use.

So, Could All zk-SNARKs… be coSNARKs?

Collaborative zk-SNARKs depend on the compatibility of the underlying zk-SNARKs with secure multi-party computation (MPC). The efficiency of this integration is determined by the “MPC-friendliness” of the zk-SNARK. This property reflects how well the proof generation process of a zk-SNARK can be adapted to a distributed, multi-party setting without incurring significant performance overhead.

How to Define MPC-Friendliness of a zk-SNARK?

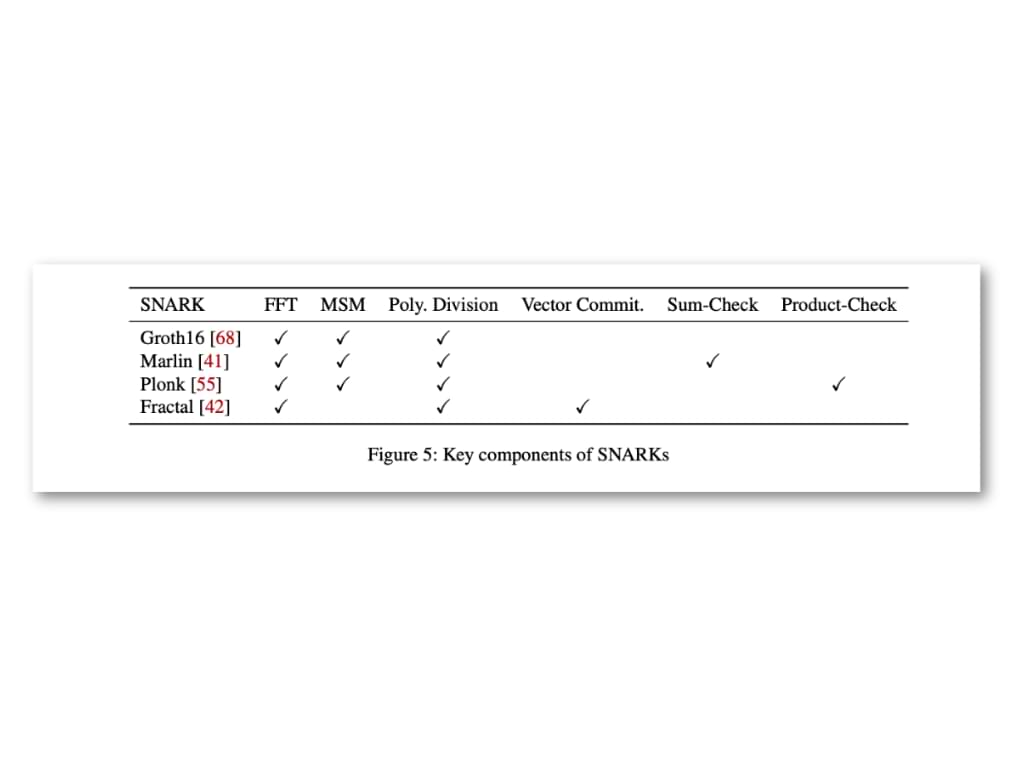
The proof generation process in zk-SNARKs typically involves complex algebraic operations, such as multi-scalar multiplications, polynomial commitments, and fast Fourier transforms (FFTs). Adapting these operations to an MPC setting requires that they support secure distributed computation efficiently. Not all zk-SNARK constructions are equally suited for this adaptation.

What Are the Most “MPC-Friendly” zk-SNARKs?

Boneh and Ozdemir’s work demonstrates that different zk-SNARKs exhibit varying degrees of MPC-friendliness:

• Highly MPC-friendly constructions: Proof systems like Groth16 and Marlin are identified as particularly suitable for collaborative zk-SNARKs. These systems rely on algebraic operations that can be efficiently distributed using MPC protocols, such as Shamir secret sharing or authenticated shares. Groth16, in particular, benefits from low communication overhead and minimal interaction requirements.

• Moderately MPC-friendly constructions: Systems like Plonk, while highly efficient in single-prover settings, incur higher communication costs in MPC due to their reliance on operations like sum-checks and product-checks. These operations require additional communication between parties, reducing their overall efficiency.

• Less MPC-friendly constructions: This includes zk-SNARKs that depend heavily on non-linear operations or cryptographic primitives, which introduce significant overhead in secure multi-party computation settings. For instance, Boneh and Ozdemir identify the Fractal proof system as less MPC-friendly when compared to others, as it relies on hash-based vector commitments and non-linear operations that result in increased communication and computation costs. Specifically, Fractal’s use of Merkle-tree-based commitments requires multiple hashing steps, making it less suitable for efficient MPC adaptation without incurring performance trade-offs. Additionally, certain pairing-intensive schemes with complex non-linear components may also fall into this category, though the authors focus primarily on the detailed evaluation of Fractal in this context.

The State of coSNARKs

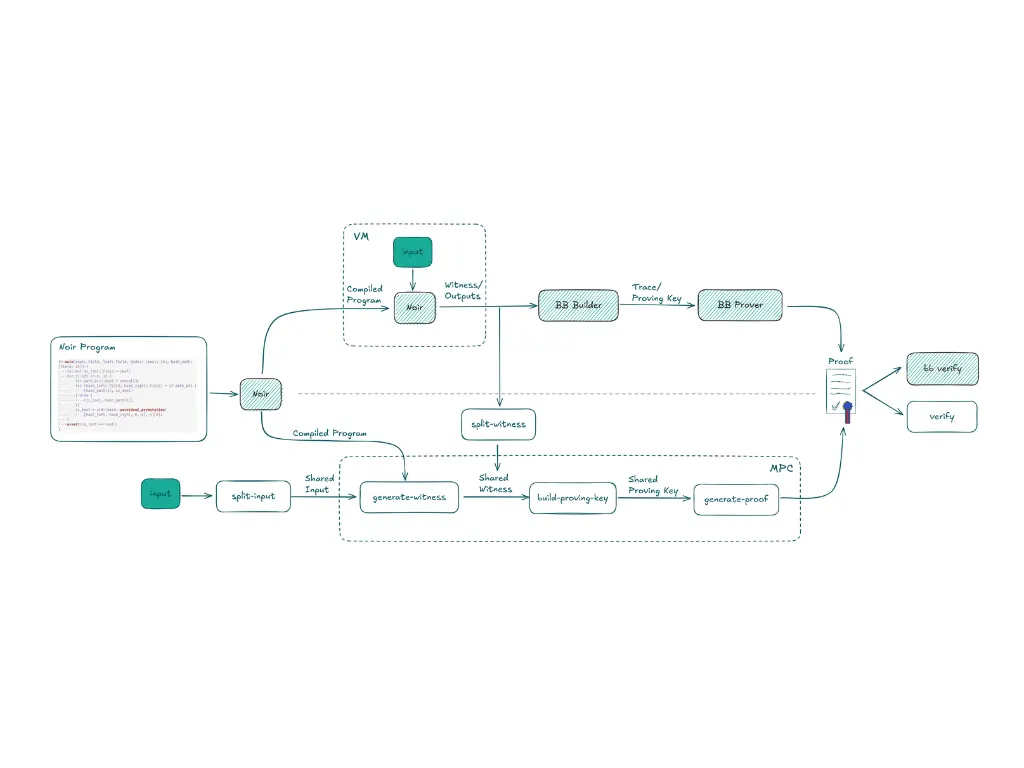
So far, the team that has championed coSNARKs and built tooling around it is TACEO. They built Co-Circom, coNoir, and more recently, they built the first production-ready coSNARKs and generated the first proofs with real-world data in their alphanet.

What’s Co-Circom?

Co-Circom provides tools to adapt Circom circuits for secure multi-party computation (MPC), enabling privacy-preserving proof generation and distributed trust. It currently supports Groth16 for efficient proof creation and is compatible with existing Circom libraries and SNARKjs. Future improvements include Plonk support and optimisations for the MPC-VM.

And coNoir?

Leveraging Noir’s intermediate representation (ACIR), coNoir enables efficient secret sharing, witness generation, and proof creation while maintaining compatibility with Barretenberg’s proving system. The tooling supports basic field operations on BN254 and can compute functions like Poseidon hashes. Future plans include expanded arithmetic capabilities, support for black-box functions, and enhanced witness extension methods.

Production-Ready coSNARKs

During Devcon7, TACEO utilised coSNARKs for a cryptographic social graph application in collaboration with Cursive and PSE. Participants exchanged contact information via NFC-enabled devices, generating zk-SNARKs to validate interactions while preserving privacy. coSNARKs delegated proof creation to a distributed MPC network to address mobile device constraints, ensuring efficient proof generation. Over 15,000 coSNARKs were produced, supporting features like leaderboards for participant engagement.

Conclusion

Although the development and research on coSNARKs are still in their nascent stages, the intersection of ZK and MPC is promising. We will keep a close eye on the research that will likely emerge on this front in the coming quarters. To keep up with advancements in coSNARKs and ZK in general, take a look at our State of ZK Report.